Семен Спивак, доктор физико-математических наук, профессор, заведующий кафедрой Башкирскоко государственного университета;

Светлана Абдюшева, кандидат физико-математических наук, доцент Башкирскоко государственного университета

Две взаимно противоположные задачи возникают при использовании марковских процессов в моделировании. Прямая задача есть вычисление вероятностей состояний и других характеристик процесса. Она предполагает параметры моделей известными. Обратная задача состоит в оценивании параметров на основании экспериментальных данных.

Настоящая статья посвящена постановке и решению обратных задач оценивания параметров в марковских моделях, используемых в медицинском страховании.

Ряд широко известных приложений использует подход, позволяющий применять теорию марковских процессов для моделирования ситуации, которая позволяет рассмотреть поведение системы со многими состояниями. Примерами могут служить задачи, связанные со всевозможными системами массового обслуживания, с рекламой, задачи надежности, а также различные приложения к биологии, химии, физике и т. п. Широкое применение этот подход получил и в актуарной практике, когда модель многих состояний используется для описания состояния застрахованного лица.

При математическом моделировании на основе марковских процессов возникают две взаимно противоположные задачи. Прямая задача состоит в расчете вероятностей соответствующих состояний и других характеристик процесса. Параметры модели при этом предполагаются известными. Обратная задача состоит в определении параметров модели на основе известных из эксперимента результирующих характеристик процессов.

В марковской модели исходные параметры – это интенсивности или силы перехода из состояния в состояние. Когда речь идет о задачах массового обслуживания или о страховых моделях, то эти интенсивности заранее, как правило, неизвестны. Статистическую же информацию о некоторых выходных данных для ряда моделей можно найти в литературе как в зарубежной, так и в отечественной.

Рассмотрим подробнее некоторые аспекты актуарного анализа.

Актуарные расчеты – это система расчетных методов, построенных на математических и статистических закономерностях. Они являются основой для регламентации страховых отношений между страховщиком и страхователями, для расчета тарифов по любому виду страхования, для определения доли участия каждого страхователя в формировании страхового фонда, для определения и анализа расходов на страхование конкретного объекта, себестоимости страховой услуги. Основными актуарными характеристиками являются нетто-премия, страховые фонды и потоки выплат.

Самые большие трудности, которые возникают при расчете актуарных характеристик, связаны с вычислением вероятности наступления страхового события.

Премии и резервы для страховых контрактов (особенно долгосрочных) основываются на текущем значении платежей в соответствии с полисом. Обычно страховое событие, время и (или) сумма каждого платежа неизвестны заранее. Они зависят от некоторых случайных событий. Как правило, все сводится к вычислению ожидаемого значения этой текущей величины, которая и зависит от вероятности наступления соответствующего события.

Как уже отмечалось выше, многие традиционные задачи актуарного анализа можно рассматривать в терминах процессов многих состояний. В таком случае предполагается, что в любой момент времени индивид может находиться в одном из перечисленных состояний. Текущее состояние индивида может быть связано с какими-либо денежными потоками (выплатами). Возникает задача количественной оценки влияния состояния индивида на денежные потоки, то есть оценки вероятности его нахождения в том или ином состоянии.

Для расчета вероятностей наступления какого-либо события как нельзя лучше подходит схема марковского процесса.

В случае актуарных расчетов простейшая ситуация включает всего два состояния застрахованного индивида – «жив» и «умер». Переход из одного состояния в другое возможен только в одном направлении (рис. 1).

  

Рисунок 1

Модель двух состояний

 

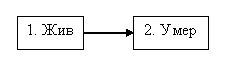
 Для простого пожизненного аннуитета страховые пособия выплачиваются, пока индивид находится в состоянии 1, и прекращаются после перехода в состояние 2. В случае полного полиса страхования жизни премии выплачиваются, пока страхователь находится в состоянии 1, а выплата по смерти осуществляется при переходе в состояние 2. Подходы к вычислению актуарных величин в этих случаях просты и хорошо известны.

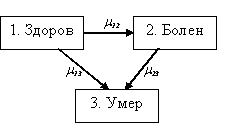
Более сложная ситуация возникает для процессов с дополнительными состояниями, как, например, в схеме, где имеются три возможных состояния – «здоров», «болен» и «умер» (рис. 2), которая обычно используется для описания состояния индивида, застрахованного по полису наступления нетрудоспособности. В этом случае премии (взносы) выплачиваются, пока страхователь находится в состоянии 1, а выплаты осуществляются до тех пор, пока он находится в состоянии 2.

  

Рисунок 2

Модель трех состояний

 

 

 

 

 

 

  

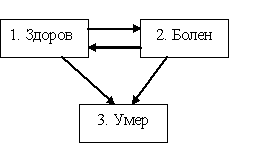
Актуарные расчеты для этого примера более трудны, так как индивид может несколько раз переходить из состояния 1 в состояние 2 и обратно. Поэтому зачастую полагают, что переход из состояния 2 в состояние 1 невозможен. При выполнении свойства Маркова такая задача также хорошо решается.

Однако применение марковских моделей для страховых сделок не всегда правомерно. Одно из затруднений, которое встречается, – это слишком большое число возможных состояний системы. Для страхования жизни это состояния здоровья индивида, которые непосредственно зависят от его возраста. Очевидно, что интенсивности перехода из состояния «здоров» в состояние «болен» сильно различаются для человека 20–30 и 50–60 лет.

Ошибки в расчетах характеристик также могут зависеть от длительности страхового полиса. Например, если страховой полис заключается на 20 лет, то характеристики в конце срока будут сильно отличатся от исходных.

Один из возможных подходов в такой ситуации – использование схемы полумарковских процессов. Стохастическая модель, в которой будущее процесса зависит от времени перехода в текущее состояние, называется полумарковской.

Аппроксимацию марковской системы полумарковской можно провести путем представления каждого состояния в виде совокупности двух и более подсостояний. Это будет означать, что возраст индивида необходимо разбить на периоды, в которые интенсивности заболеваний можно считать постоянными. Это приведет к тому, что в марковской модели параметры, которыми являются интенсивности переходов из состояния в состояние, будут представлять собой кусочно-постоянные функции.

Рассмотрим сначала общий вид марковского процесса и его свойства.

Обозначим Х(t) состояние индивида в возрасте t (t³0). Определим стохастический процесс, как {Х(t), t³0}. Предположим, что имеется конечное число состояний, пронумерованных 1,2,...n, то есть процесс имеет пространство состояний {1,2,…,n}. Тогда {Х(t), t³0} – марковский процесс, если для любых s, t ³0 и i, j, x(u)Î{1,2,…n}, , то есть будущее процесса (после момента времени s) зависит только от состояния в момент времени s и не зависит от истории процесса до момента s.

Применимость марковского предположения зависит отчасти от уровня детализации в описании состояний. Например, рассмотрим процесс с тремя состояниями, изображенный на рис. 2. В этом случае марковское предположение может быть неприменимо. Будущее здоровье недавно заболевшего индивида, очевидно, отличается от здоровья лица того же возраста, которое болеет долгий период времени. (Решение этой проблемы обсуждалось выше.)

Определим функцию вероятности перехода  и положим, что  для любого t³0.

Предположим также существование пределов , i,jÎ{1,2…n}, i¹j.

При i¹j m_ij – это интенсивность перехода их состояния i в состояние j. Легко увидеть, что при s, t, u ³0

 

(1)  i,jÎ{1,2,…n}.

 

Функции (1) известны как уравнения Колмогорова-Чепмэна.

При вычислении актуарных значений необходимы функции вероятности перехода. Интенсивности переходов и функции вероятности перехода связаны с прямыми и обратными уравнениями Колмогорова:

 

(2)

 

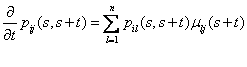
(3) ,

 

соответственно, с граничными условиями , где

В общем случае, эти системы дифференциальных уравнений должны быть разрешены численно для получения функций вероятности переходов.

Точные выражения для функций вероятности переходов можно получить, когда  для всех t. Такой марковский процесс является однородным по времени, или стационарным. Предположение, что интенсивности переходов постоянны, подразумевает, что время, проведенное в каждом состоянии, имеет экспоненциальное распределение, а также, что функции одинаковы для всех s, и их можно обозначить просто .

В случае кусочно-постоянных функций интенсивностей переходов интервал времени, на котором проводится исследование, можно разбить на промежутки постоянства параметров. Для того чтобы решение – функции вероятностей переходов были непрерывны, необходимо «склеивать» решение на отдельных участках.

Когда интенсивности переходов известны, случай сводится к прямой задаче – решению уравнений Колмогорова-Чепмэна. Для моделей с постоянными интенсивностями это не очень сложно независимо от числа возможных состояний системы. Но если интенсивности переходов неизвестны, возникает обратная задача, то есть задача оценивания интенсивностей переходов по статистическим данным.

Оценка интенсивностей переходов является сложной проблемой, особенно если задача имеет большую размерность. Так, если имеется n состояний, то из них можно образовать C_n² различных пар (i,j), i,j=1..n, i¹j. Причем каждой паре (i,j) соответствует две интенсивности перехода m_ij и m_ji. Таким образом, всего требуется найти 2C_n²=n(n-1) статистические оценки интенсивностей переходов, представляющие собой не параметры, а функции возраста x.

Поэтому эта проблема должна решаться при определенных предположениях, а именно:

1. Интенсивности перехода m_ij аппроксимируем кусочно-постоянными функциями. Для этого весь период наблюдения разбиваем на такие временные интервалы, чтобы в пределах каждого из них можно было бы считать интенсивности переходов постоянными. Пусть – один из таких интервалов, а m_ij@m_ij – для всех.

2. Наблюдения проводим за индивидами, фактический возраст x которых принадлежит интервалу.

3. Каждому индивиду соответствует независимая реализация случайного процесса.

4. Поведение индивида не зависит от того, каким образом наблюдение за ним было начато, и от того, по какой причине оно прекратилось.

Еще одно предположение, которое существенно облегчит решение поставленной задачи, – это наличие полной информации об истории каждого наблюдаемого индивида. Так в [1] модель многих состояний применяется для описания процесса страхования утраты трудоспособности. Оценки интенсивностей переходов осуществляются методом максимального правдоподобия по полным данным – предполагаются известными все его переходные состояния и время нахождения в них.

Однако наличие полных данных – случай крайне редкий. В задачах страхования жизни экспериментальная информация представлена, как правило, лишь в так называемых таблицах смертности. Из них можно извлечь информацию о значениях вероятности смерти в определенном возрасте для индивидов определенной группы.

Таблица смертности строится на основе следующих данных:

рассматривается достаточно большая группа людей, например, 100 000, одинакового возраста, наблюдаемых некоторое время;

через l_x обозначается число индивидов возраста x, оставшихся в живых от первоначальной совокупности в 100 000 человек;

далее вычисляется значение d_x=l_x-l_x+1 – число умерших в течение года после возраста x;

вероятность любому из наблюдаемых индивидов умереть в течение года после возраста x равна q_x=d_x/l_x;

соответсвенно p_x=1-q_x – вероятность прожить индивиду возраста x в течение года.

Одним из наиболее распространенных методов статистического оценивания является метод наименьших квадратов, состоящий в том, что оценка неизвестных параметров определяется из условия минимума нормы вектора ошибок (вектора невязок).

Рассмотрим пример использования описанного выше подхода для оценки смертности курящих и некурящих людей. Статистические данные для расчетов были взяты из [2].

В [2] приводятся таблицы смертности для четырех групп людей: курящие и некурящие мужчины, курящие и некурящие женщины. Фрагмент одной из таблиц приведен ниже (табл. 1).

  

Таблица 1

Таблицы смертности для некурящих (мужчин)

Age x	lx	dx	qx
25	96 570	65	0,00067
26	96 505	63	0,00066
27	96 442	62	0,00065
28	96 380	62	0,00065
29	96 318	64	0,00066
30	96 254	65	0,00067
31	96 189	67	0,00070
32	96 122	70	0,00072
33	96 052	73	0,00076
34	95 979	77	0,00080
35	95 902	82	0,00086

   

Для исследования были взяты данные таблиц для курящих и некурящих мужчин возраста от 30 до 45 лет.

По таблицам можно найти вероятности смерти в каком-либо возрасте по формулам, приведенным выше.

Данной ситуации можно сопоставить процесс с тремя состояниями, схема переходов в котором представлена на рис. 3.

  

Рисунок 3

Модель «курящий – некурящий»

 

  

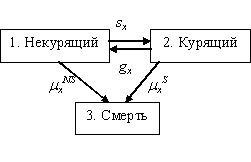
Этой схеме соответствуют следующие предположения и допущения:

1. Имеются три возможных состояния. Каждый индивид может находиться в любом из них. Два «живых» состояния – 1 и 2, и состояние «смерть», которое является невозвратным.

2. Рассматривается возможность того, что некурящие люди могут начать курить, а потом бросить, а также того, что уже курящие люди могут бросить курить.

3. В любом из «живых» состояний люди могут умирать как из-за того, что курят (или курили когда-то), так и от других причин.

4. В рассматриваемом возрастном интервале [30,45] все интенсивности переходов можно считать постоянными.

В описанной модели четыре неизвестных параметра – интенсивности переходов s_x, g_x, m_x^NS, m_x^S.

По таблицам смертности находим значения вероятностей смерти в возрасте x. Для схемы на рис. 3 это вероятности переходов из состояния 1 в состояние 3 и из состояния 2 в состояние 3.

Уравнения Колмогорова-Чепмэна для данной схемы имеют вид:

 

 

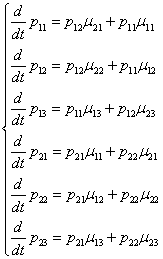
Нормировочное условие – .

Начальные условия для этого примера могут быть заданы, исходя из двух соображений:

1. В начальный момент () индивид не курит, то есть находится в состоянии 1.

2. В начальный момент () индивид не курит, то есть находится в состоянии 2:

 

 

Методом наименьших квадратов получены следующие численные оценки интенсивностей перехода: m₁₂ = 0,0164, m₂₁= 0,0592, m₁₃=0,00107, m₂₃= 0,00921.

Для рассматриваемого случая параметры модели будут зависеть от возраста х. В общем случае они могут зависеть от длительности пребывания в том или ином состоянии (то есть отличаться для индивидов одного возраста, но с разной предысторией). Этот случай, очевидно, более сложный и требует наличия более обширной информации о наблюдаемых индивидах.

Итак, будем считать, что интенсивности переходов из одного состояния в любое другое отличаются для различных возрастов х, то есть m_ij @m_ij(х).

Возраст индивида x задан как дискретная величина (1 год, 2 года, …, 15 лет, 16 лет и т. д.). Таким образом, полагается, что в течение одного года жизни интенсивности переходов не меняются, то есть функции m_ij(х) есть кусочно-постоянные функции.

Если рассматривать возраст индивида x не как дискретную величину, а как непрерывную, можно попытаться построить «гладкие» функции интенсивностей переходов, то есть рассчитать значения этих функций в дискретных точках по имеющимся данным, а затем аппроксимировать эти точки по возможности более гладкой кривой.

Для рассматриваемой схемы в качестве подкласса, на котором ищется приближенное решение, можно взять отрезок [0;1] (это оправдано априорными соображениями). Методом подбора были получены численные оценки интенсивностей переходов [2] и проведена их аппроксимация. Получены следующие результаты:

m₁₂ Î [0,000171;0,00036];

m₂₁Î [0,000121;0,00051];

m₁₃Î [0,000671;0,00086];

m₂₃ Î[0,001180;0,00193].

  

Таблица 2

Возраст x	P13_стат	P13_рез	P23_стат	P23_рез
25	0,00067	0,000670	0,00118	0,001180
26	0,00066	0,000661	0,00117	0,001169
27	0,00065	0,000650	0,00118	0,001181
28	0,00065	0,000651	0,00121	0,001211
29	0,00066	0.000661	0,00128	0,001281
30	0,00067	0,000670	0,00135	0,001351
31	0,00070	0,000700	0,00145	0,001450
32	0,00072	0,000720	0,00154	0,001541
33	0,00076	0,000760	0,00165	0,001651
34	0,00080	0,000800	0,00178	0,001781
35	0,00086	0,000859	0,00193	0,001931

  

Поскольку полученное решение не является единственным, необходимо оценить диапазон изменения значений m_ij, в пределах которого будет получено хорошее приближение статистических данных. Анализ соответствующей марковской схемы и системы уравнений позволяет предположить, что сильные изменения (увеличения или уменьшения) m₁₃ и m₂₃ приведут к существенным изменениям в значениях p₁₃ и p₂₃. Изменения в m₁₂ и m₂₁ будут влиять на эти величины гораздо в меньшей степени.

В ходе численного эксперимента были получены следующие результаты: уменьшение и увеличение значений параметров m₁₂ и m₂₁ в большом диапазоне (до двух порядков) приводит к очень незначительным изменениям в расчетных вероятностях (в пределах 1–3%), вероятности p₁₂ и p₂₁ меняются сильно, пропорционально изменениям m₁₂ и m₂₁. Большие изменения m₁₃ и m₂₃ приводят к пропорциональным изменениям p₁₃ и p₂₃. Такая зависимость обусловлена особенностями модели.

Все вышесказанное позволяет сделать вывод о том, что для данной модели решение обратной задачи требует дополнительной информации, помимо статистических данных о вероятностях смерти. Такой информацией могут служить, например данные о длительностях пребывания в состояниях 1 и 2 (рис. 2). Установлению большей определенности в нахождении решения существенно может помочь оценка вероятностей p₁₂ и p₂₁ для разных возрастов. Например, данные социологического опроса курящих и некурящих людей могли бы стать источником такой информации.

Решение обратной задачи, соответствующей марковской схеме, не будет единственным. Это является характерным для большинства обратных задач.

Существуют различные методы нахождения оценочных интервалов, то есть выделения подпространства в пространстве допустимых решений. Каждая точка такого подпространства удовлетворяет системе уравнений, начальным условиям и системе ограничений.

  

Рисунок 4

 

  

Таким образом, можно придавать параметрам различные значения из подпространства решений и получать одинаково хорошее описание статистических данных. Такое варьирование параметров можно осуществлять как произвольно, так и используя известные функциональные зависимости между параметрами, например для процесса с тремя состояниями (рис. 4) сила смертности для людей заданной возрастной группы будет зависеть от интенсивностей переходов следующим образом:

 

.

 

Отсюда видно, что при любом выборе значений трех параметров существует другой выбор, который обеспечивает в точности то же значение m(t). Так, если , то можно получить такое же m(t), полагая . В отсутствие априорной информации о величинах параметров можно выбрать любые значения. Однако поставленная цель – просто найти наилучшее значение m(t) , основываясь на трехстадийной модели.

Наличие неоднозначности в решении обратной задачи приводит к возникновению следующего вопроса: можно ли осуществить такой выбор из подпространства решений, чтобы по возможности оптимизировать характеристики рассматриваемого процесса?

Этот вопрос станет предметом дальнейших исследований.

 

Литература:

1. Страхование от несчастных случаев на производстве: актуарные основы. Под ред. В. Н. Баскакова. М.: Academia. 2001.

2. Benjamin B., Michaelson R., Mortality differences between smokers and non-smokers, Journal of the Institute of Actuaries, Vol. 115, Part III, № 461, 1988.